【回归分析】关于相关与回归——笔者通过自己的文章教你如何化繁为简！

对于相关和回归的关系，教材是这么说的：

相关用于说明两变量之间的关系方向和密切程度，没有主次之分；回归更进一步用于定量刻画两变量在数值上的依存关系，可以依据专业拟定主次。

我们在学习和工作中还常见下面这些表述：

（1）相关是回归的基础，无相关就无回归。

（2）相关程度越高，回归方程的拟合程度就越好。

（3）能进行回归分析的变量之间存在相关关系。

（4）相关是一种双向变化关系，回归是一种单向变化关系。

（5）对于新数据，可先做散点图，求出相关系数，对于确有相关关系的变量再进行回归分析。

（6）相关系数（r）和回归系数（β）的方向一致，可以相互推算。

（7）研究两个变量的相互关系用相关分析，研究两个变量的依存关系用回归分析。

正因为教材中的定义和平时常见的表述，在实际应用中两者容易混淆，对于自己的数据，不知道是该用相关，还是该用回归，或者该用哪种回归。

问题一：

没有相关关系就不能做回归分析吗？

我们知道在回归分析之前，首先需要了解变数间是何种相关关系，才能选择适当的回归模型。

但大千世界关系复杂，看似无序的两者，可能存在某种特定关系，因此很多时候看似无序的数据，经过分层、分组、多因素或合适的模型处理，才能发现有意义的关系，并建立回归模型。

因此，在理解「相关是回归的基础，无相关就无回归」的表述时，要辨别是没有发现数据潜在的相关关系，还是数据之间真的没有相关关系。

问题二：

一种相关关系只能建立一种回归模型吗？

回归分析的方法一直在不断进步，新的回归模型不断涌现，一组具有相关关系的数据，如何选择最合适的回归模型呢？

这不是几句话能说清楚的，笔者建议一定要自己多看文献才能融会贯通。结合数据的实际用途，了解数据的相关因素，选择合适的回归模型，解决工作中的实际问题。

问题三：

相同的相关关系（相关系数 r），回归模型是否会一致？

回归模型相同，数据的关系就一样吗？

相关系数（r）和回归系数（β）数值的大小存在着内在的联系，这是导致这两个统计概念难以辨析的原因。通常 r 绝对值越大的两组变量间，β 的绝对值也越高。但相同的回归模型，可能有不尽相同的相关关系（见图 1）。

因此，分析前应绘制散点图，从专业角度考虑数据间的关系。

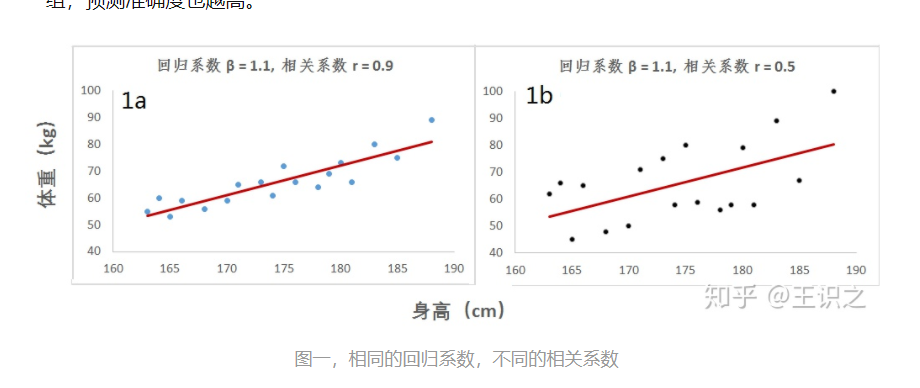图片来源：相关与回归，傻傻分不清 - 王识之的文章 - 知乎 https://zhuanlan.zhihu.com/p/80744389

辨析相关与回归的关系，最重要的还是为了在合适的场景中应用。

笔者以自己一次数据分析的过程，讲述一下自己对于相关与回归的理解。

数据分析实例

数据来源于真实世界的一个横断面研究数据库，之前在研究血清铁蛋白（Ferritin）与肥胖、糖尿病等慢病的关系时，发现铁蛋白与性别、年龄以及机体的炎症状态等相关。

笔者希望通过分析，了解血清铁蛋白在人群中的分布特点，为下一步研究建立理论依据。

第一步，按照教材提示，首先建立血清铁蛋白的散点图。

作者先选择了年龄作为横坐标（图 2-1），之所以选择年龄，是因为这是连续变量，并在之前研究中发现其与铁蛋白有着某种相关关系，从散点图中可以看出血清铁蛋白呈现非正态分布特征。

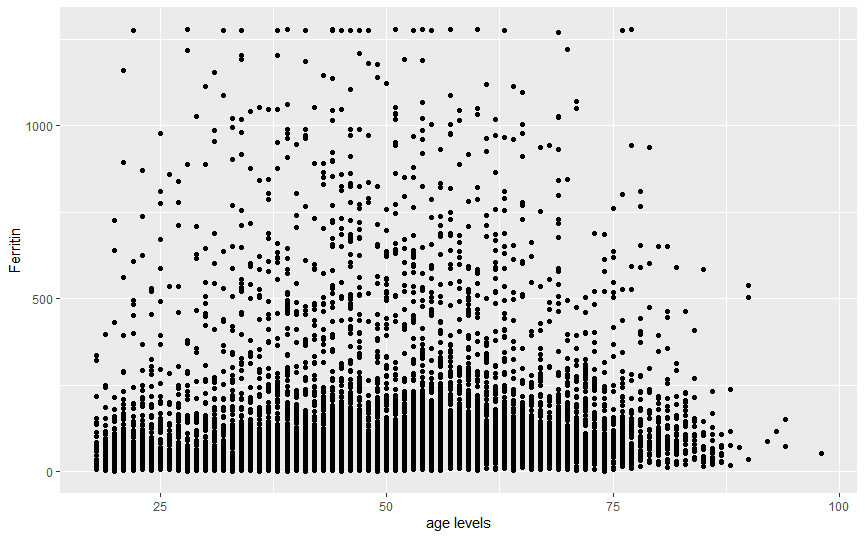
图2-1 铁蛋白与年龄散点图

第二步，简单直线相关分析需要数据呈正态分布，我们可以通过对数转换，将偏态数据正态化，转换后的铁蛋白与年龄散点图见图 2-2。我们尝试进行了线性相关分析，显示铁蛋白与年龄似乎有一定相关性。

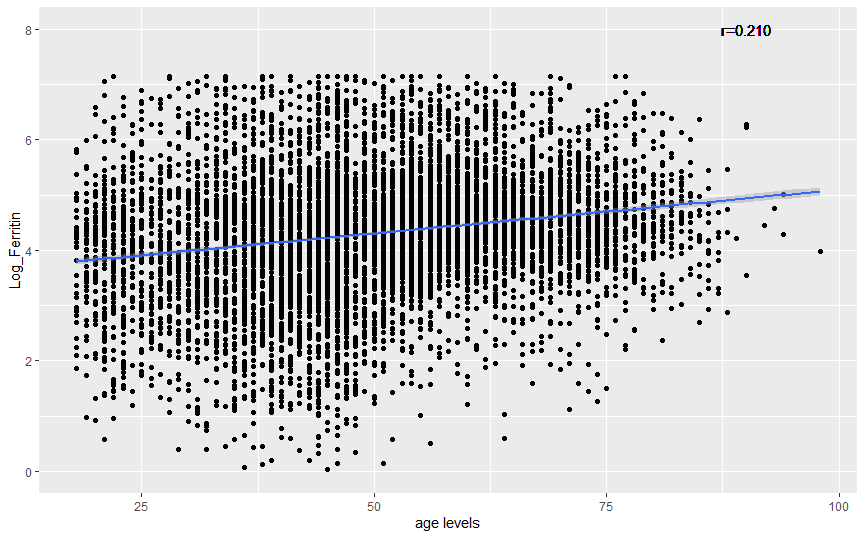
图 2-2 Log 转换后铁蛋白与年龄散点图

第三步，这时，我们考虑引入第二个相关因素——性别。

之前阅读文献时发现男性和女性铁蛋白水平有显出差异，性别是分类变量，通过分组绘制散点图并分别绘制回归线（见图 2-3），可见不同性别组铁蛋白的分布有很大的差异，甚至男性和女性的相关关系呈现出截然相反的方向。

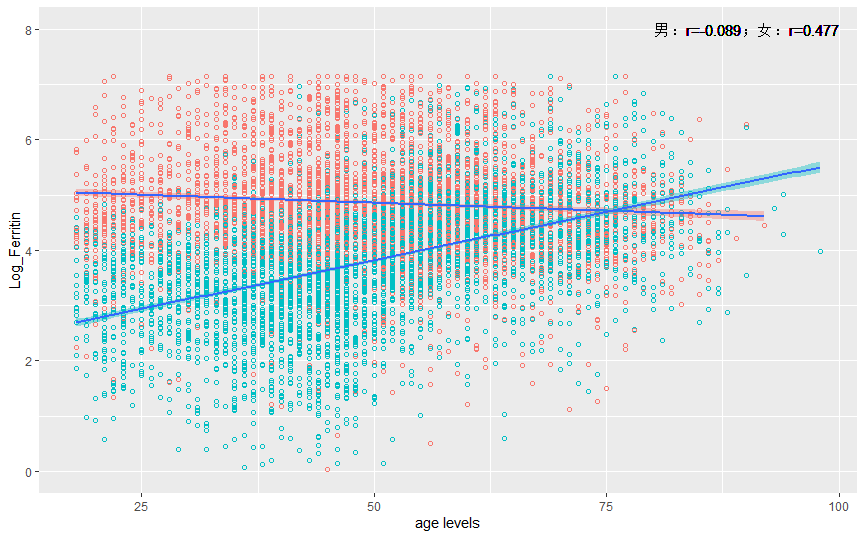
图 2-3 性别分组的 Log 转换后铁蛋白与年龄散点图

第四步，那有没有可能是不同的年龄阶段相关关系有所不同，而简单线性回归模型掩盖了不同年龄阶段的不同关系？

我们尝试选择局部加权回归（LOESS）看看效果（见图 2-4），由于 LOESS 对于变量分布形态没有过多限制，所以我们用原始的铁蛋白数据进行分析，图形显示男性呈现倒 U 型关系，女性呈现 S 型关系。

铁蛋白在青中年男性（30-40 岁）的峰值可能和其肌肉含量、营养状态相关，在女性 50 岁之后有个明显升高，可能与更年期状态变化相关。有文献指出月经周期是更年期前女性铁蛋白水平低的原因，这样相关关系和专业知识、文献报道呼应上了。

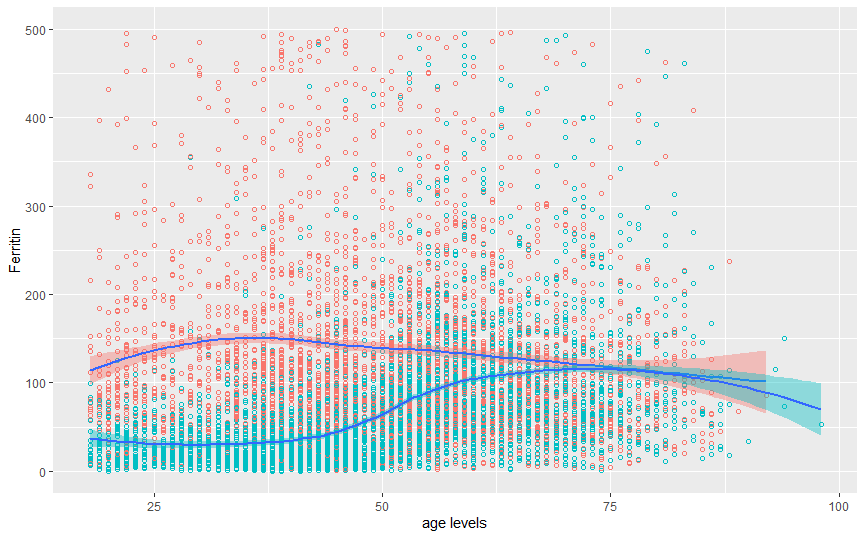
图 2-4 性别分组的铁蛋白与年龄 LOESS 模型散点图

第五步，引入第三个相关因素——炎症状态。

恰巧数据库中有反应炎症状态的标志物 C 反应蛋白（CRP）数据，这时候再选择多因素线性回归，可能就不合适了，我们将 CRP 作为影响因素纳入广义加法模型（GAMLSS），见图 2-5 和图 2-6。

可见年龄增高、CRP 浓度增加，血清铁蛋白的人群水平变化增加，数据可信区间增大。这样我们可以进一步通过不同模型的比较，选择最为合适的模型对数据进行描述和回归建立预测模型。

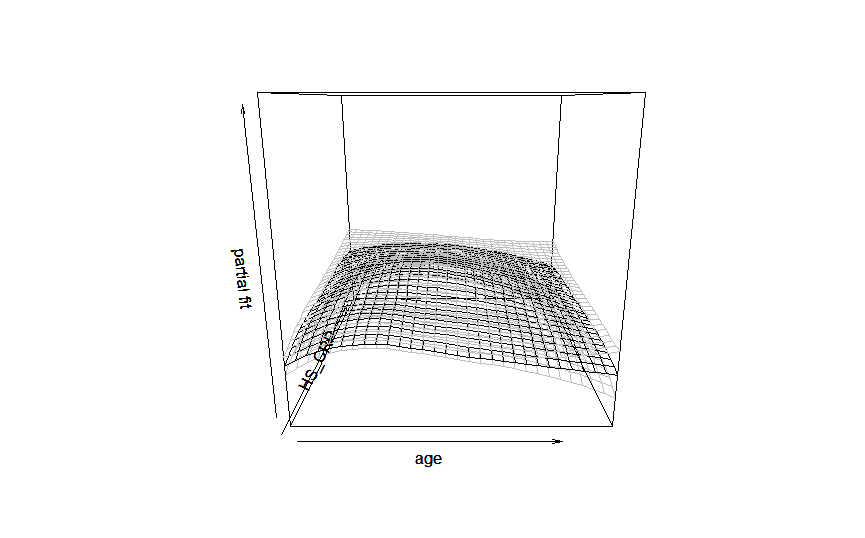
图 2-5 男性铁蛋白与年龄、C 反应蛋白关系的 GAMLSS 回归模型图

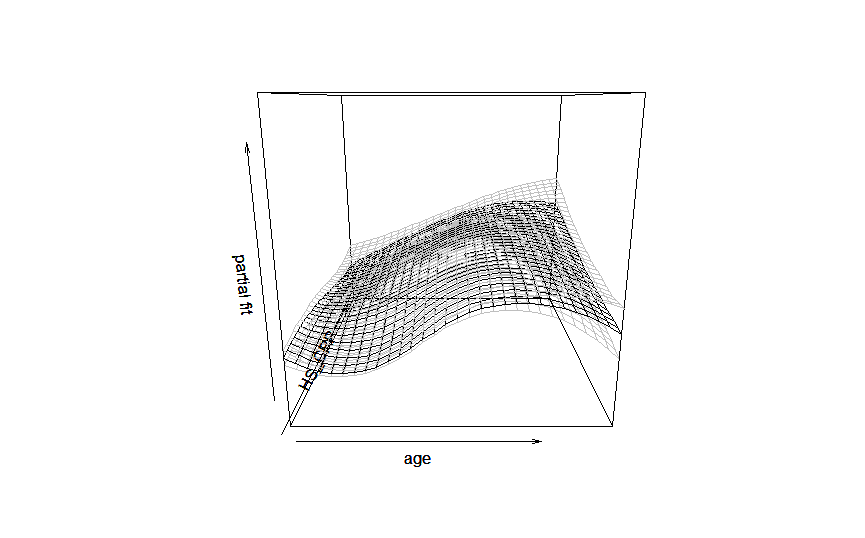
图 2-6 女性铁蛋白与年龄、C 反应蛋白关系的 GAMLSS 回归模型图

可见，通过文献阅读、专业知识判断，加强对于数据的理解，数据之间的相关关系会更加明朗，建立的回归模型会更加合适。

数据呈现出的表观上的相关关系，通过选择合适的方法，如分组、分层、多因素处理，可以拟合出不同的回归模型，通过对建立的不同回归模型进行比较，最终选择出有利于实际工作的相关关系和回归模型，解决临床中遇到的问题。

丁香科研精品技能课 1 分钱学

内含外泌体、SCI 写作、文献检索

综述指导教学等海量科研课

👇👇👇