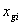三种基因表达差异的显著性分析方法

互联网2013-09-06

15920

相关专题: DNA微阵列基因表达数据分析

用于检测基因表达水平的 DNA 微阵列实验，应用之一是比较实验，目的是比较两个条件下的基因表达差异，从中识别出与条件相关的特异性基因，例如，识别可用于肿瘤分型的特异基因等。

为了提高实验的可靠性，对于同一样本，往往有两次或更多次的重复实验，但是，由于 DNA 微阵列的费用仍然很昂贵，不可能重复足够多的次数来满足实验数据分析的要求，因此需要采用统计方法来分析这些数据。对于这些表达数据的分析，目的就是要识别在两个条件下有显著表达差异的基因。

何谓显著表达差异?通常是指一个基因在两个条件中表达水平的检测值在排除实验、检测等因素外，达到一定的差异，具有统计学意义，同时也具有生物学意义。

常用的分析方法有三类，第一类称之为倍数分析，计算每一个基因在两个条件下的 Ratio 值，若大于给定阈值，则为表达差异显著的基因;第二类方法采用统计分析中的 t 检验和方差分析，计算表达差异的置信度，来分析差异是否具有统计显著性;第三类是建模的方法，通过确定两个条件下的模型参数是否相同来判断表达差异的显著性，例如贝叶斯方法。

倍数分析

早期基于 cDNA 微阵列技术的比较实验，用倍数来分析基因表达水平差异，即计算基因在两个条件下表达水平的 Ratio 值。用表示基因 g 在条件 i 下的表达水平测量值，因此， Ratio 值为，可表示基因 g 在条件 1 和 2 下的表达水平差异。对于 cDNA 微阵列实验，是将两个条件下的样本混合后与 cDNA 微阵列进行杂交实验，得到的是成对数据，对每次实验得到的数据计算，最后计算重复实验的平均。

而对于寡核苷酸芯片，首先分别计算两个样本的重复实验的归一化表达水平的平均值，然后计算其 Ratio 值。当 =1 时，基因 g 的表达水平没有改变，而 <1 或 >1 意味着基因 g 在两个条件下存在表达差异，特别是 <1 表示基因在条件 1 是下调的，而 >1 ，表示在条件 1 是上调的。

在具体应用中，如果一个基因的平均表达水平在两个条件下的变化超过一个常数，典型的常数是 2 ，即 >2 或 <1/2 ，则认为该基因的表达差异是显著的。

然而，对表达数据仔细考察后可以发现，这样简单的 2 倍法并不能产生最优的结果，因为因子 2 在不同的表达水平上有相当不同的显著性。

对于低表达水平的基因，其信噪比太低，用 2 倍法作为判断条件太宽松，而对于高表达基因，条件又太苛刻，往往小于 2 就具有生物学意义。在具体应用中，并没有明确的阈值，往往根据分析的具体要求由数据分析者自行确定。

t 检验

于两个条件下的多次重复实验，为了判断基因的表达差异是否具有显著性，在应用中较多的是采用假设检验，包括两个条件下的 t 检验和多个条件下的方差分析( ANOVA )，这里仅仅介绍 t 检验，关于 ANOVA 请参考相应的统计分析书籍。

零假设为

，即假设两个条件下的平均表达水平是相等的，与之对应的备选假设是

。 t 统计量的计算公式如下：
<center> <img alt="三种基因表达差异的显著性分析方法" height="57" src="http://img.dxycdn.com/trademd/upload/asset/meeting/2013/09/06/A1378380609.png" width="162" /></center> <center> </center>

(8-6) 其中三种基因表达差异的显著性分析方法，，为某一条件下的重复实验次数,Xgij是基因g在第i个条件下第j次重复实验的表达水平测量值。根据统计量值，可以得到 p 值，它表示在零假设成立的情况下，出现该数据的概率。

如果 p 值小于给定的显著性水平，就拒绝零假设，即认为基因 g 在两个条件下的表达差异是显著的。因为在 t 检验中，两个总体平均值之间的距离被样本的标准差归一化，可以克服固定倍数阈值方法的一些缺点。

然而，对于 DNA 微阵列数据的 t 检验的基本问题是，即使用当前的高通量检测技术，实验仍然花费很大或者实验过程很冗长，重复次数经常较小， =2 、 3 的小样本仍然非常普通。

由于样本量小，导致总体方差被严重低估，得到的 t 值就较大，因此会导致较高的假发现率 (FDR ， False Discovery Rate) ，即通过 t 检验得到的结果中表达差异不显著的基因数目较多。这样，需要更好的分析方法来克服这些缺点。

在 t 假设检验中，经常使用的显著性水平是 p =0.01 ，其意思是在零假设正确的情况下，从总体中进行 100 次抽样，允许有 1 次不满足零假设。

对于 DNA 微阵列实验，检测的基因数目巨大，如果微阵列上有 10000 个基因，采用 p =0.01 ，将会有 100 个基因是由于偶然性而被错误认为是有表达差异显著的。这个数目已经可能对后续的生物学分析产生很大的干扰，从而导致 t 检验分析结果的不可靠或失去意义。

为了解决这个问题，可以对 t 检验进行改进，降低由于分母上方差小而带来的错误，因此对 t 检验的计算公式修改如下：

假设

的分布是独立于基因表达水平的。因为较低的表达水平会使

的值较小，导致

值变化较大。为了保证

独立于基因表达水平，在分母上增加 S0 ，增加 S0 后可以降低

的方差。通过对设计的一组对照样本的分析，可以确定阈值，

大于阈值的基因被认为是表达差异显著的。

8.3.3 贝叶斯分析

由于 DNA 微阵列数据噪声大、波动大，而且在大量数据的背后还有很多相关变量不能被观察到，因此，贝叶斯方法可以用来分析微阵列表达数据。贝叶斯分析可以简单描述如下：

<center> <img alt="三种基因表达差异的显著性分析方法" height="22" src="http://img.dxycdn.com/trademd/upload/asset/meeting/2013/09/06/A1378380591.png" width="226" /></center> <center> </center> (8-10) 其中， P(M|D) 表示由观测数据集 D 得到参数化模型 <center> </center> <center> <img alt="三种基因表达差异的显著性分析方法" height="22" src="http://img.dxycdn.com/trademd/upload/asset/meeting/2013/09/06/A1378380595.png" width="77" /></center>

为真的概率，称为后验概率; P(M) 称为先验概率，表示在没有得到任何数据之前所估计的模型 M 为真的概率; P(D|M) 是指似然度，表示从模型 M 得到一个观测数据集 D 的概率。贝叶斯推断是通过参数估计和模型选择来实现任务的，最常用的方法是最大后验概率 (MAP) 估计和最大似然 (ML) 估计。

在用贝叶斯方法分析表达数据时，首先假设在给定条件下，一个基因的表达水平测量值是独立的，并满足正态分布。根据经验，这一假设是合理的，特别是表达水平的对数大致服从对数正态分布。对于重复实验，也可以引入伽玛分布、高斯 / 伽玛混合分布等。一个基因在一种条件下的表达测量值可以用一个正态分布

<center> <img alt="三种基因表达差异的显著性分析方法" height="25" src="http://img.dxycdn.com/trademd/upload/asset/meeting/2013/09/06/A1378380607.png" width="81" /></center> <center> </center> 来建模。对于每个基因在每一种条件下，都对应有一个双参数模型 <center> </center> <center> <img alt="三种基因表达差异的显著性分析方法" height="25" src="http://img.dxycdn.com/trademd/upload/asset/meeting/2013/09/06/A1378380600.png" width="81" /> ，似然函数可以由下式给出：</center> <center> </center> <center> <img alt="三种基因表达差异的显著性分析方法" height="63" src="http://img.dxycdn.com/trademd/upload/asset/meeting/2013/09/06/A1378380610.png" width="586" /> (8-11)</center> <center> </center> i 取遍所有的重复测量，重复测量次数为 n ，C表示归一化常数。似然度取决于充分统计量 n 、

和

分别表示重复次数、 n 次重复实验的平均值和方差。先验概率分布

的选择有几种，一般采用共扼先验分布。先验分布的四个超参数构成向量

，则 <center> <img alt="三种基因表达差异的显著性分析方法" height="28" src="http://img.dxycdn.com/trademd/upload/asset/meeting/2013/09/06/A1378380593.png" width="328" /> (8-12)</center> <center> </center>

超参数