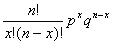蛋白质库的设计和筛选---概率计算
丁香园
3713
1. 简介
自然进化是一个产生给定样品的很多“变体”随后在“变体”中选择那些最适于特定环境或特定目的的过程。自然进化是机体内遗传突变或重组进而产生新蛋白质变体的结果。抗体的产生很好的描述了这种进化过程:天然抗体库在机体内产生大量的各种 “变体”,这些变体被不断地取样测试,那些最适于与特定配体结合的变体被从天然库中筛选出来进行下一轮的优化。蛋白质变体的选择需要基因型与表型的耦合——这在自然进化中是自然发生的,但在实验室进行人工蛋白质进化时却很难实现。在过去的 10 年中,随着很多策略的发展可以产生更好说明的大蛋白质库来联结基因型与表现型,与此同时也发展了许多新型功能筛选方法和选择策略,蛋白质工程的工具发生 了革命性进展(见参考文献 [1] 和 [2])。
本章的目标是将与蛋白质库的产生以及利用这些库进行筛选的策略相关的统计与概率计算以组合生物学家的语言进行阐述,以利于这些计算方法的应用。本章的目的也是要揭示这些计算与库的产生及筛选过程的相关性。当我们设计一个基于蛋白质库筛选的蛋白质工程实验时,必须平衡好产生一个最具多样性的蛋白质库的科学价值与实际筛选或选择策略方法局限性之间的关系。与蛋白质库表征相关的统计与概率问题是重要的,并且这些问题随着不同的应用而变化。我们还给出了实验偏差的检测,来帮助评价筛选前后蛋白质库的质量及偏差的出现情况。我们将会看到对于筛选库问题的简单分析可以揭示出很重要,甚至有时是违反直觉的结果,这些信息反过来可以使我们的实验设计得到快速改进,并且提供给我们解 释结果的更强有力的依据。
我们首先讨论对于设计蛋白质库相关的一些重要参数,如蛋白质库的大小、组分的偏好性、密码子简并性及编码多样性。然后,我们将继续讨论一系列常见的问题, 对于每个问题都给出相关的明晰的数学处理。为了阐明公式的应用我们通常会提供数值解范例。如果所需数学工具比较复杂费时,我们会给实验者提供 Excel 文档文件来输入合适的变量。我们所提出的问题都具有足够的普遍性适用于基于蛋白库的多样性系统而不只适用于一些特例。
我们必须提起注意下面给出的很多结果只适用于参数是足够大或足够小的情形,如果应用于其他地方则可能导致错误结论。我们也会提供一些特殊条件的情形。
基于蛋白质库策略数学处理的补充性工作还包括 DNA 混编(shufflin g ) 的数学模型,特别是 Moore 和 Mamnas ( 见参考文献 [ 3 ]~ [ 6 ] ) 及 Sun ( 见参考文献 [7]) 的重要工作,最近还有 Blackburn 及其同事 [8] 的工作。上述后者的工作也提供了库的等概率结果的库表征的数学处理;作为处理库的非等概率结果的库表征的开端,我们也 提出了一个相同处理方法。参考文献 [ 8 ] 还提出了一个易错(error- prone) PCR 产生库的多样性的评估方法,更重要的是为用户提供了简捷的计算机程序。
1.1 库的产生及筛选的参数
蛋白库的设计及筛选过程中有一些参数必须事先确定,如所需库的大小,特定应用的库的表征以及筛选策略所附加的限制条件。尽管可能导致概念及实验误差,这些参数还是可以凭直觉提出。这些参数的数学意义将在 3.1 节中进一步讨论,以帮助实验者更好地计划及实施基于库的实验工作。
1.1.1 蛋白质库大小的设计
无论组合生物学家利用自然产生的蛋白质库还是合成库,首先必须确定库的大小,以利于将来能够精确评价筛选结果。自然产生的蛋白质库包括天然抗体集合以及来自某种细胞器(或器官)和某一机体的整个蛋白质组。合成库一般源于某一种蛋白质或一类同源蛋白,这些蛋白质可以是高度多样性的。当前用来产生这些合成库的技术包括饱和突变(saturation metagenesis);利用 PCR 的随机突变;“基因混编”,即将类似来源的 DNA 片段组合在一起;“定向”突变,即改变特定区域的 DNA 编码;以及序列的非同源、随机重组策略等(非同源重组可参见文献 [1]、[2] 及 [9])。对于设计合意的合成库的大小,下列考虑是必需的。
对于小的多肽库(如 10 个氨基酸长的十肽),有 2010 ( ≈ 1.02X1013,原文错误——译者注)种可能的氨基酸组合。同样的计算适用于蛋白质中特定位置包含有 10 个随机分布的氨基酸的情形。然而,由于密码简并性,对 于 10 个氨基酸的多肽存在着更多的编码可能性,我们必须产生大于 2010 的 DNA 多样性库来编码一个合适的包括 2010 种不同多肽的组合,这样才能根据每个多肽的编码可能性表征出其合理的分布。例如,在一个随机 DNA 库中,对于丝氨酸、精氨酸和亮氨酸(Ser、Arg 和 Leu,以下同,用英文三字母缩写来表示 20 种不同氨基酸)存在 6 种编码可能性,这是最高的冗余度。这样,编码一个 10-Ser 多肽是高度冗余的,有 610=6X107 可能组合都编码这种 10-Ser 肽,然而对于非简并的 10-Met 多肽只存在唯一的编码组合。(像 Met 这样)非简并氨基酸只用 1/64 的三联码来唯一编码,密码简并性使得实际应用的 DNA 库必须大于不考虑简并性计算出来的结果以确保非简并氨基酸有一定的机会出现。更明确的说,在这个例子中我们必须编码 6410 ( ≈1.2 X 1018 ) 种可能的 DNA ( 三联码)序列来确保 10-Met 多肽可能有一定的概率出现。不幸的是,编码 1.2 X 1018 种十肽的 DNA 库质量大约是 2 mg,这样的量对于大多数研究机构来说是太大了。值得提出的是利用上述对于十肽编码的分析我们可以考虑更长的多肽或蛋白质其中任意 10 个氨基酸(连续的或间隔的)需要被改变的情形。因此,在计划 构建多肽或蛋白质库时密码子的简并性是必须考虑到的。
1.1.2 偏好性蛋白质库
我们常常需要使 DNA 库具有编码偏好性。这样做最显然的优势是:① 降低终止密码子的影响,终止子在非偏好性库中会产生大量非功能性序列(表 8.1 );② 使 ( DNA ) 库向需要的氨基酸组分倾向;③ 降低不同氨基酸在密码子表征上的差别,使得各种氨基酸在库中具有更加均一的表征。具有 “ NNC” 或 “NNT” (N 表示 4 种核苷酸中任意一种)重复序列的 DNA 库可以使密码子从 64 种变为 16 种,同时消除了 3 种终止子(表 8.1)。然而这样做使得 5 种氨基酸(Met、Trp、Gin、Glu 和 Lys) 没有被编码,导致了编码多样性的损失。利用 “NNC” 或 “NNT”重复编码的缺点是某些密码子在大肠杆菌(最常用蛋白质表达宿主)中密码子应用偏好性较差 [ 10 ]。“ NNC/T ” 编码也是常用的,它补偿了密码子利用偏好性问题,但使密码子数目增加了一倍而没增加编码的氨基酸种类。因为在完全随机的编码库中( “NNN”),得到没有终止子的概率随着简并位点的增加而急剧下降(表 8.1 ) 从而导致低质量库的产生,所以上述无终止子的编码是完全值得牺牲一些氨基酸多样性的。另外的做法是用 “NNC/G” 或 “NNT/G”,这样所有 20 种氨基酸都被编码且只包含一个终止子;“ NNC/G” 密码子对大肠杆菌具有较好的应用性。这样,得到无终止子产物的概率显著大于用 “NNN” 编码的库。因此,当需要产生多重简并性氨基酸时,序列中的终止子对于库的质量是非常有害的,如果所用的筛选策略是需时费力并且很昂贵的话,应该尽力避免终止子。
实验者经常需要在特定的位置产生特殊的氨基酸序列。尽管有现成软件来实现这一工作,我们还是可以手工完成这样的寡核苷酸偏好性设计。例如,T.J.Magliery ( www. chemistry, ohio-state. edu/magliery/publicatioin. html ) 写的 “ Mixed CodonWorksheet” 就是一个基于 Excel 文件的设计程序,把一个需要的氨基酸列入表中,不同的可能性会被计算出来,使得实验者可以根据需要选择最合适的密码子。一些寡核苷酸合成供应商也可以根据需要提供各种可能比例的核苷酸,使得实验者可以偏好性选择核苷酸分布从而使特定氨基酸得到偏好。这种策略可以按照需要用来减少或者增加编码表征中的差异性。
在理想状况下,一个具有偏好性的库可以从“三核苷酸联码”中构建 [11],其中 3 个特定核苷酸共价连接在一起构成“砌块” (building block) ,每个 “砌块” 编码一个特定氨基酸,并且可以被用来以需要的比例混合放在特定的位置进行寡核苷酸合成。由于这种做法是非简并的,所以可以将 DNA 库的大小减至正好和感兴趣的蛋白质库大 小一样。利用三核苷酸的优势已经被特别提出(见参考文献 [12]~ [14]),但由于这种方法近来只是处于商业化过程中(Glen Research Sterling,VA ; 及 Metkinen Oy,Kuusisto,Finland) , 完成的工作还相对较少。
1.1.3 库大小的限制
在具体实践中,可实现的库大小上限为毫克量级,这对于 30 bp ( 相应于 10 个氨基酸)的双链 DNA 分子来说大约为 3 X 1016 个。然而,蛋白质表达一般是基于载体 DNA 来实现的。一个典型的表达载体大概是 3000 bp 长。因此,在毫克量级的理想状况下,对于一个 3000 bp 的载体可以最多产生约 3 X 1014 个双链 DNA 分子。这样,现实中对于 10 个完全随机氨基酸位置(1.2 X 1018 种可能性)的上限仅仅是所有可能性的一小部分 ( 更多关于库表征计算的细节参见 3.1.2)。这样,我们只能够部分的探索完全随机的十肽库(或者编码 10 个完全随机的氨基酸的蛋白质),完全不可能全面研究一个哪怕仅仅是平均大小的蛋白质。这意味着需要用两种方式产生蛋白质库。第一种,靶蛋白本身可被 “完全”随机化;这种情形下,所得蛋白质库仅代表所有可能性的一个子集 ( 见 1.2 )。如果我们需要了解一个给定功能的野生型蛋白质序列中的相对重要性信息的话,这种做法会非常有效。筛选出的蛋白质中那些统计学上不常变化的残基提示其对于保留所选择的性质具有关键意义;这种提示很像利用多重天然蛋白序列比对来确定功能氨基酸残基。在第二种方法中,序列随机性被加以限制;仅仅特定残基(无论是否邻近)被完全随机化和(或)偏好性被引入随机化中以限制可能性数目。这样可以得到性质和大小完全确定的蛋白质库;而且库的大小可以被 1.1 节所述方法限制。如果我们需要对于库中的每个成员进行筛选(而不仅仅从一个子集合中取样)的话,则库的大小还可以进一步被限制。
1.2 蛋白质库的表征
与所需库的大小(内容)相关联的是我们要考虑对于特定应用的库表征。要使一个库的筛选效率高,编码的独立变体数必须与筛选策略及能力相匹配。如 1.1 节所述,产生大量和多样性的 DNA 库本身并不难。实际上我们必须限制库的大小才能使之能够被充分地筛选。筛选所需表型(与基因型相关联)的工具相对于产生 DNA 库更加难以发展,这是因为这些工具不像操纵 DNA 的方法那样可以广泛应用。因此,筛选具有不同功能的蛋白质,必 须建立起多样化的筛选策略(见参见文献 [2] )。
一般来说,实验者进行手工操作可以筛选成百上千种蛋白质变体;自动化可以增加几个数量级的蛋白质变体个数。体内方法可以快速筛选几千到几十亿个蛋白质变体。无细胞(cell- free) 系统可能是更强有力的实验技术(计算方法除外),可以使我们筛选 1014 个蛋白质变体。显而易见,上述任何一种方法能够处理的蛋白质变体量与理论上可以产生的蛋白质变体量相比是非常局限的,需强调说明必须将库的设计与筛选能力结合起来。实验者或许需计算一个样本中实际蛋白质变体的表征;3.1 节提供了这样的数学工具。
1.3 确定实验偏差
库筛选会产生大量的序列信息(在核酸或者氨基酸水平),必须加以精确阐明。例如,对于库的质量评价需要确定偏差。在库的设计及构建完成后,进行筛选实验前要选出几个样品进行 DNA 测序。在一个突变位点观察到的与期待的核苷酸分布之间的差异可以用来评价是否存在显著偏差。显著偏差会显示出错误的密码子分布,其来源于寡核苷酸合成失误或者由于野生型序列导致的随机突变设计偏差。偏差也意味着出现了一定量的非期待选择;这样或许需要改变实验系统,如变换表达宿主细胞或者利用体外系统进行表达。阐明实验误差的工具基于 X2 检验,将在 3.2 节中详述。
进一步的 X2 检验应用还可以比较筛选实验前后的 DNA 序列来揭示筛选实验造成的密码子分布差别。我们需要观察一个特定残基筛选后的突变频率偏差,或者在一个需要偏好的位点出现特定氨基酸的偏差。应用 X2 检验实验者可以确定观察到的偏差是否显著,因此,来确定施加的选择压力对富集某一特定的分布是否足够强。
2. 材料
对于许多计算问题,Excel 工作单(图 8.1~图 8.4 ) 可以提供很好的重复性。通过网页 http : //ww w. esi. umontreal. ca /pelletjo/ 可以直接得到与图中相同的工作单。 这些 Excel 工作单严格遵循此章结构。图 8.1 和 图 8.2 给出两例等概率和非等概率的计算结果,由于它们是基于相同 λ 参数的泊松分布,因此得到类似的处理。图 8.3 ( 再次给出等概率和非等概率的两例)是基于不同 λ 参数的泊松分布。框内单元数据需要用户输入。灰色单元给出答案。




4. 注
1. 对于问题 A 和 B 的解答 8. 3. 1. 1 的 1 ) 和 2 ) 依赖于伯努里(Bernoulli) 随机变 数求和的泊松近似理论,这一理论主要是说,如果所有在方程(8.9 ) 和方程(8.14 ) 中定义的 ks 值都很小,那么没有在样本中出现
的变量的个数将近似服从参数。泊松分布 [ 关于数学具体算法请参见参考文献 [ 15 ] 的第 10 章,特别是关于
多项分布的例 10.2 ( B) ] 。
根据参考文献 [ 16 ] 的第 252 页,泊松近似在 n≥20,λ≤10 时效果最佳。
2. 没有出现的变量个数近似服从参数的泊松分布,这里,λi 可被定义为

注意,给出特定的 λi,λ 值可被直接计算而无须计算 λi。
3. 用 Excel 计算泊松分布在分布系数 λ 很大时依然适用。在这种情况下,可以简单地运用均值等于 λ 和方差等于 λ 的正态分布,也就是 N ( λ,λ ) 替代。这一技巧的举例说明见图 8.2。
4. 由于泊松分布的特点

5. 问题 C 的解答是基于次数计数这一随机变量服从变量的二项分布的泊松近似。这里,根据参考文献 [16],泊松近似在 n>20,λ< 10 时效果最佳。
6. 在样本中得到一个特定变量 i 的事件为一定次数 r 的概率服从参数为 m ( 样本容量)和 1/n ( 选取变量 i 的概率,任何时刻一个变量被选取是随机的)的二项分布。这一二项分布可以很好地近似为参数泊松分布,而且计算起来也更容易。
7. 见注 2。对于这种情况,λ 可以计算如下。不同于等概率情况,λi 在这里是不同的。首先,为了计算 λ,我们需要计算所有的 n = 2110 个参数 λi,这个工作量很大,但是这里包含了很多重复,这一特征可以用来简化计算。而且,让我们确定一些由五元组(n1,n2,n3,n4,n5)确定的十肽,由密码子的数量可知,它们的概率在所描述的十肽中分别为 1/64,2/64,3/64,4/64,5/64。并且有

种不同的十肽与五元组(n1,n2,n3,n4,n5)有关。这一数字解释了多肽中密码子的所有混编,也就是多肽中的氨基酸次序不需要被明确定义。它同样说明了这样一个事实,不止一个氨基酸能表现出其中的每一个概率(除了异亮氨酸,异亮氨酸是唯一一 个被 3/ 64 密码子编码的氨基酸)。我们提出的观点是,五元组包含了用来回答我们问题的关于十肽的所有信息。现在我们可以用 λ(n1,n2,n3,n4,n5)来替换 λi=(1-pi)m 的计算,因此,对于特定的十肽 i:
λi=λ(n1,n2,n3,n4,n5)=[ 1-p(n1,n2,n3,n4,n5)] m
这对于与十肽 i 相关的五元组(n1,n2,n3,n4,n5)是特定的。也就是说,对于 2110 个参数 λi,我们只需要计算 λi 中出现的不同值。λi 中一共有

个不同的值;这里,我们用了二项系数记号。
我们最后只用这 1001 个 λ(n1,n2,n3,n4,n5)值来计算,以及每个数值根据式(8.13 ) 所给出的重复次数。

这里第二,第三和第四步的求和都是定义在 8.1 中的五元组(n1,n2,n3,n4,n5)。也就是说,它们都是五套数字,这里 ni 是在 { 0,1,···,10 } 中的个数,因为它是—个十肽。同样的,p(n1,n2,n3,n4,n5)根据式
(8.16 ) 计算得到。最后一个方程给出了 λ 的近似值 ( 对于很小的 x,1 + x≈ex),这个运算要明显比从第二个方程到最后一个方程简单;通常,在计算机上计算,1 - p(n1,n2,n3,n4,n5)将趋近于 1。
8. 见注 5。这里唯一的不同是二项分布的基本事件概率不再是 1/n ( 等概率部分描述的概率),而是其他的一些基于不同的变量的概率 p。
9. 回顾显著性水平 α=0.05 的意义。这表示有 5% 的机会犯第一类错误,意味着假设为真却被拒绝。换句话说,这里有 1 : 20 的机会说明一个完美执行的试验有缺陷。
参考文献
1. Arnold, F. H. and Georgiou, G. (200 3 ) Directed Evolution Library Creation Methods and Protocols.Methodsin Molecular Biology 2 31, Humana Press, Totowa, NJ.
2. Arnold, F. H. and Georgiou, G. (2003) Directed Enzyme Evolution Screening and Selection Methods,Methodsin Molecular Biology 2 3 0, Humana Press, Totowa, NJ.
3. Moore, J. C. , Jin, H. M. , Kuchner, O. , and Arnold, F. H. ( 1 997) Strategies for the in vitro evolution ofprotein function —enzyme evolution by random recombination of improved sequences. /. Mol. Biol.272, 336-347.
4. Moore, G. L. and Maranas, C. D. (2000) Modeling DNA mutation and recombination for directed evolution experiments. J . Theor. Biol. 20 5 , 483-503.
5. Moore,G. L . ,Maranas,C. D . ,Lutz,S . ,and Benkovie,S. J. ( 2 0 0 1 ) Predicting crossover generation inDNA shuffling. Proc. NatL Acad. Sci. USA 98, 3226-3231.
6. Moore, G. L. and Maranas, C. D. ( 2002 ) Predicting out-of-sequence reassembly in DNA shuffling. /.Theor. Biol.2 1 9, 9-17.
7. Sun, F. ( 1 999) Modeling DNA shuffling./. BzoZ. 6 , 77-90.
8. Patrick, W. M. , Firth, A. E. , and Blackburn, J. M. (200 3) User-friendly algorithms for estimating complete?
ness and diversity in randomized protein-encoding libraries. Protein Eng. 16 , 451-457.
9. Bittker, J. A , I^e, R V. , Liu, J. M. , and Liu, D. R (2004) Directed evolution of protein enzymes using nonhomologous random recombinatioa Proc. Natl. Acad. Sci. USA 10 1, 7011-7016.
10. Gribskov, M. , Devereux, J. , and Burgess, R. R. (1 98 4 ) The codon preference plot: graphic analysis of protein coding sequences and prediction of gene expression. Nucleic Acids Res. 1 2, 539-549.
11. Virnekas, B. , Ge, L. , Pluckthun, A. , Schneider, K. C. , Wellnhofer, G. > and Moroney, S. E. ( 1 99 4 )Trinucleotide phosphoramidites : ideal reagents for the synthesis of mixed oligonucleotides for random mutagenesis. Nucleic Acids Res.22, 5600-5607.
12. Pelletier, J. N. > Arndt, K. M. , Pliickthun, A. , and Michnick, S. W. ( 1 999) An in vivo library-versus-library selection of optimized protein-protein interactions. Nature BiotechnoL 1 7, 683-690.
13. Braunagel, M. and Little, M. ( 1 997) Construction of a semisynthetic antibody library using trinucleotide oligos. Nucleic Acids Res. 25, 4690, 4691.
14. Gaytan, P. , Yanez,J . ,Sanchez, F . , and Soberon, X. ( 20 0 1 ) Orthogonal combinatorial mutagenesis: acodon-level combinatorial mutagenesis method useful for low multiplicity and amino acid-scanning protocols. Nucleic Acids Res. 29, E9.
15. Ross, S. ML ( 1 996) Stochastic Processes. 2nd ed. 9 John Wiley Sons, New York, NY.
16. Hogg, R. V. and Tanis, E. A. ( 1 98 3 ) Probability and Statistical Inference. 2nd eA. MacMillan, New York,NY.
17. Ross, S. M. (1998) A Fist Course in Probability. 5th ed. 9 Prentice Hall, Upper Saddle River, NJ.
自然进化是一个产生给定样品的很多“变体”随后在“变体”中选择那些最适于特定环境或特定目的的过程。自然进化是机体内遗传突变或重组进而产生新蛋白质变体的结果。抗体的产生很好的描述了这种进化过程:天然抗体库在机体内产生大量的各种 “变体”,这些变体被不断地取样测试,那些最适于与特定配体结合的变体被从天然库中筛选出来进行下一轮的优化。蛋白质变体的选择需要基因型与表型的耦合——这在自然进化中是自然发生的,但在实验室进行人工蛋白质进化时却很难实现。在过去的 10 年中,随着很多策略的发展可以产生更好说明的大蛋白质库来联结基因型与表现型,与此同时也发展了许多新型功能筛选方法和选择策略,蛋白质工程的工具发生 了革命性进展(见参考文献 [1] 和 [2])。
本章的目标是将与蛋白质库的产生以及利用这些库进行筛选的策略相关的统计与概率计算以组合生物学家的语言进行阐述,以利于这些计算方法的应用。本章的目的也是要揭示这些计算与库的产生及筛选过程的相关性。当我们设计一个基于蛋白质库筛选的蛋白质工程实验时,必须平衡好产生一个最具多样性的蛋白质库的科学价值与实际筛选或选择策略方法局限性之间的关系。与蛋白质库表征相关的统计与概率问题是重要的,并且这些问题随着不同的应用而变化。我们还给出了实验偏差的检测,来帮助评价筛选前后蛋白质库的质量及偏差的出现情况。我们将会看到对于筛选库问题的简单分析可以揭示出很重要,甚至有时是违反直觉的结果,这些信息反过来可以使我们的实验设计得到快速改进,并且提供给我们解 释结果的更强有力的依据。
我们首先讨论对于设计蛋白质库相关的一些重要参数,如蛋白质库的大小、组分的偏好性、密码子简并性及编码多样性。然后,我们将继续讨论一系列常见的问题, 对于每个问题都给出相关的明晰的数学处理。为了阐明公式的应用我们通常会提供数值解范例。如果所需数学工具比较复杂费时,我们会给实验者提供 Excel 文档文件来输入合适的变量。我们所提出的问题都具有足够的普遍性适用于基于蛋白库的多样性系统而不只适用于一些特例。
我们必须提起注意下面给出的很多结果只适用于参数是足够大或足够小的情形,如果应用于其他地方则可能导致错误结论。我们也会提供一些特殊条件的情形。
基于蛋白质库策略数学处理的补充性工作还包括 DNA 混编(shufflin g ) 的数学模型,特别是 Moore 和 Mamnas ( 见参考文献 [ 3 ]~ [ 6 ] ) 及 Sun ( 见参考文献 [7]) 的重要工作,最近还有 Blackburn 及其同事 [8] 的工作。上述后者的工作也提供了库的等概率结果的库表征的数学处理;作为处理库的非等概率结果的库表征的开端,我们也 提出了一个相同处理方法。参考文献 [ 8 ] 还提出了一个易错(error- prone) PCR 产生库的多样性的评估方法,更重要的是为用户提供了简捷的计算机程序。
1.1 库的产生及筛选的参数
蛋白库的设计及筛选过程中有一些参数必须事先确定,如所需库的大小,特定应用的库的表征以及筛选策略所附加的限制条件。尽管可能导致概念及实验误差,这些参数还是可以凭直觉提出。这些参数的数学意义将在 3.1 节中进一步讨论,以帮助实验者更好地计划及实施基于库的实验工作。
1.1.1 蛋白质库大小的设计
无论组合生物学家利用自然产生的蛋白质库还是合成库,首先必须确定库的大小,以利于将来能够精确评价筛选结果。自然产生的蛋白质库包括天然抗体集合以及来自某种细胞器(或器官)和某一机体的整个蛋白质组。合成库一般源于某一种蛋白质或一类同源蛋白,这些蛋白质可以是高度多样性的。当前用来产生这些合成库的技术包括饱和突变(saturation metagenesis);利用 PCR 的随机突变;“基因混编”,即将类似来源的 DNA 片段组合在一起;“定向”突变,即改变特定区域的 DNA 编码;以及序列的非同源、随机重组策略等(非同源重组可参见文献 [1]、[2] 及 [9])。对于设计合意的合成库的大小,下列考虑是必需的。
对于小的多肽库(如 10 个氨基酸长的十肽),有 2010 ( ≈ 1.02X1013,原文错误——译者注)种可能的氨基酸组合。同样的计算适用于蛋白质中特定位置包含有 10 个随机分布的氨基酸的情形。然而,由于密码简并性,对 于 10 个氨基酸的多肽存在着更多的编码可能性,我们必须产生大于 2010 的 DNA 多样性库来编码一个合适的包括 2010 种不同多肽的组合,这样才能根据每个多肽的编码可能性表征出其合理的分布。例如,在一个随机 DNA 库中,对于丝氨酸、精氨酸和亮氨酸(Ser、Arg 和 Leu,以下同,用英文三字母缩写来表示 20 种不同氨基酸)存在 6 种编码可能性,这是最高的冗余度。这样,编码一个 10-Ser 多肽是高度冗余的,有 610=6X107 可能组合都编码这种 10-Ser 肽,然而对于非简并的 10-Met 多肽只存在唯一的编码组合。(像 Met 这样)非简并氨基酸只用 1/64 的三联码来唯一编码,密码简并性使得实际应用的 DNA 库必须大于不考虑简并性计算出来的结果以确保非简并氨基酸有一定的机会出现。更明确的说,在这个例子中我们必须编码 6410 ( ≈1.2 X 1018 ) 种可能的 DNA ( 三联码)序列来确保 10-Met 多肽可能有一定的概率出现。不幸的是,编码 1.2 X 1018 种十肽的 DNA 库质量大约是 2 mg,这样的量对于大多数研究机构来说是太大了。值得提出的是利用上述对于十肽编码的分析我们可以考虑更长的多肽或蛋白质其中任意 10 个氨基酸(连续的或间隔的)需要被改变的情形。因此,在计划 构建多肽或蛋白质库时密码子的简并性是必须考虑到的。
1.1.2 偏好性蛋白质库
我们常常需要使 DNA 库具有编码偏好性。这样做最显然的优势是:① 降低终止密码子的影响,终止子在非偏好性库中会产生大量非功能性序列(表 8.1 );② 使 ( DNA ) 库向需要的氨基酸组分倾向;③ 降低不同氨基酸在密码子表征上的差别,使得各种氨基酸在库中具有更加均一的表征。具有 “ NNC” 或 “NNT” (N 表示 4 种核苷酸中任意一种)重复序列的 DNA 库可以使密码子从 64 种变为 16 种,同时消除了 3 种终止子(表 8.1)。然而这样做使得 5 种氨基酸(Met、Trp、Gin、Glu 和 Lys) 没有被编码,导致了编码多样性的损失。利用 “NNC” 或 “NNT”重复编码的缺点是某些密码子在大肠杆菌(最常用蛋白质表达宿主)中密码子应用偏好性较差 [ 10 ]。“ NNC/T ” 编码也是常用的,它补偿了密码子利用偏好性问题,但使密码子数目增加了一倍而没增加编码的氨基酸种类。因为在完全随机的编码库中( “NNN”),得到没有终止子的概率随着简并位点的增加而急剧下降(表 8.1 ) 从而导致低质量库的产生,所以上述无终止子的编码是完全值得牺牲一些氨基酸多样性的。另外的做法是用 “NNC/G” 或 “NNT/G”,这样所有 20 种氨基酸都被编码且只包含一个终止子;“ NNC/G” 密码子对大肠杆菌具有较好的应用性。这样,得到无终止子产物的概率显著大于用 “NNN” 编码的库。因此,当需要产生多重简并性氨基酸时,序列中的终止子对于库的质量是非常有害的,如果所用的筛选策略是需时费力并且很昂贵的话,应该尽力避免终止子。
实验者经常需要在特定的位置产生特殊的氨基酸序列。尽管有现成软件来实现这一工作,我们还是可以手工完成这样的寡核苷酸偏好性设计。例如,T.J.Magliery ( www. chemistry, ohio-state. edu/magliery/publicatioin. html ) 写的 “ Mixed CodonWorksheet” 就是一个基于 Excel 文件的设计程序,把一个需要的氨基酸列入表中,不同的可能性会被计算出来,使得实验者可以根据需要选择最合适的密码子。一些寡核苷酸合成供应商也可以根据需要提供各种可能比例的核苷酸,使得实验者可以偏好性选择核苷酸分布从而使特定氨基酸得到偏好。这种策略可以按照需要用来减少或者增加编码表征中的差异性。
在理想状况下,一个具有偏好性的库可以从“三核苷酸联码”中构建 [11],其中 3 个特定核苷酸共价连接在一起构成“砌块” (building block) ,每个 “砌块” 编码一个特定氨基酸,并且可以被用来以需要的比例混合放在特定的位置进行寡核苷酸合成。由于这种做法是非简并的,所以可以将 DNA 库的大小减至正好和感兴趣的蛋白质库大 小一样。利用三核苷酸的优势已经被特别提出(见参考文献 [12]~ [14]),但由于这种方法近来只是处于商业化过程中(Glen Research Sterling,VA ; 及 Metkinen Oy,Kuusisto,Finland) , 完成的工作还相对较少。
1.1.3 库大小的限制
在具体实践中,可实现的库大小上限为毫克量级,这对于 30 bp ( 相应于 10 个氨基酸)的双链 DNA 分子来说大约为 3 X 1016 个。然而,蛋白质表达一般是基于载体 DNA 来实现的。一个典型的表达载体大概是 3000 bp 长。因此,在毫克量级的理想状况下,对于一个 3000 bp 的载体可以最多产生约 3 X 1014 个双链 DNA 分子。这样,现实中对于 10 个完全随机氨基酸位置(1.2 X 1018 种可能性)的上限仅仅是所有可能性的一小部分 ( 更多关于库表征计算的细节参见 3.1.2)。这样,我们只能够部分的探索完全随机的十肽库(或者编码 10 个完全随机的氨基酸的蛋白质),完全不可能全面研究一个哪怕仅仅是平均大小的蛋白质。这意味着需要用两种方式产生蛋白质库。第一种,靶蛋白本身可被 “完全”随机化;这种情形下,所得蛋白质库仅代表所有可能性的一个子集 ( 见 1.2 )。如果我们需要了解一个给定功能的野生型蛋白质序列中的相对重要性信息的话,这种做法会非常有效。筛选出的蛋白质中那些统计学上不常变化的残基提示其对于保留所选择的性质具有关键意义;这种提示很像利用多重天然蛋白序列比对来确定功能氨基酸残基。在第二种方法中,序列随机性被加以限制;仅仅特定残基(无论是否邻近)被完全随机化和(或)偏好性被引入随机化中以限制可能性数目。这样可以得到性质和大小完全确定的蛋白质库;而且库的大小可以被 1.1 节所述方法限制。如果我们需要对于库中的每个成员进行筛选(而不仅仅从一个子集合中取样)的话,则库的大小还可以进一步被限制。
1.2 蛋白质库的表征
与所需库的大小(内容)相关联的是我们要考虑对于特定应用的库表征。要使一个库的筛选效率高,编码的独立变体数必须与筛选策略及能力相匹配。如 1.1 节所述,产生大量和多样性的 DNA 库本身并不难。实际上我们必须限制库的大小才能使之能够被充分地筛选。筛选所需表型(与基因型相关联)的工具相对于产生 DNA 库更加难以发展,这是因为这些工具不像操纵 DNA 的方法那样可以广泛应用。因此,筛选具有不同功能的蛋白质,必 须建立起多样化的筛选策略(见参见文献 [2] )。
一般来说,实验者进行手工操作可以筛选成百上千种蛋白质变体;自动化可以增加几个数量级的蛋白质变体个数。体内方法可以快速筛选几千到几十亿个蛋白质变体。无细胞(cell- free) 系统可能是更强有力的实验技术(计算方法除外),可以使我们筛选 1014 个蛋白质变体。显而易见,上述任何一种方法能够处理的蛋白质变体量与理论上可以产生的蛋白质变体量相比是非常局限的,需强调说明必须将库的设计与筛选能力结合起来。实验者或许需计算一个样本中实际蛋白质变体的表征;3.1 节提供了这样的数学工具。
1.3 确定实验偏差
库筛选会产生大量的序列信息(在核酸或者氨基酸水平),必须加以精确阐明。例如,对于库的质量评价需要确定偏差。在库的设计及构建完成后,进行筛选实验前要选出几个样品进行 DNA 测序。在一个突变位点观察到的与期待的核苷酸分布之间的差异可以用来评价是否存在显著偏差。显著偏差会显示出错误的密码子分布,其来源于寡核苷酸合成失误或者由于野生型序列导致的随机突变设计偏差。偏差也意味着出现了一定量的非期待选择;这样或许需要改变实验系统,如变换表达宿主细胞或者利用体外系统进行表达。阐明实验误差的工具基于 X2 检验,将在 3.2 节中详述。
进一步的 X2 检验应用还可以比较筛选实验前后的 DNA 序列来揭示筛选实验造成的密码子分布差别。我们需要观察一个特定残基筛选后的突变频率偏差,或者在一个需要偏好的位点出现特定氨基酸的偏差。应用 X2 检验实验者可以确定观察到的偏差是否显著,因此,来确定施加的选择压力对富集某一特定的分布是否足够强。
2. 材料
对于许多计算问题,Excel 工作单(图 8.1~图 8.4 ) 可以提供很好的重复性。通过网页 http : //ww w. esi. umontreal. ca /pelletjo/ 可以直接得到与图中相同的工作单。 这些 Excel 工作单严格遵循此章结构。图 8.1 和 图 8.2 给出两例等概率和非等概率的计算结果,由于它们是基于相同 λ 参数的泊松分布,因此得到类似的处理。图 8.3 ( 再次给出等概率和非等概率的两例)是基于不同 λ 参数的泊松分布。框内单元数据需要用户输入。灰色单元给出答案。




4. 注
1. 对于问题 A 和 B 的解答 8. 3. 1. 1 的 1 ) 和 2 ) 依赖于伯努里(Bernoulli) 随机变 数求和的泊松近似理论,这一理论主要是说,如果所有在方程(8.9 ) 和方程(8.14 ) 中定义的 ks 值都很小,那么没有在样本中出现
的变量的个数将近似服从参数。泊松分布 [ 关于数学具体算法请参见参考文献 [ 15 ] 的第 10 章,特别是关于
多项分布的例 10.2 ( B) ] 。
根据参考文献 [ 16 ] 的第 252 页,泊松近似在 n≥20,λ≤10 时效果最佳。
2. 没有出现的变量个数近似服从参数的泊松分布,这里,λi 可被定义为

注意,给出特定的 λi,λ 值可被直接计算而无须计算 λi。
3. 用 Excel 计算泊松分布在分布系数 λ 很大时依然适用。在这种情况下,可以简单地运用均值等于 λ 和方差等于 λ 的正态分布,也就是 N ( λ,λ ) 替代。这一技巧的举例说明见图 8.2。
4. 由于泊松分布的特点

5. 问题 C 的解答是基于次数计数这一随机变量服从变量的二项分布的泊松近似。这里,根据参考文献 [16],泊松近似在 n>20,λ< 10 时效果最佳。
6. 在样本中得到一个特定变量 i 的事件为一定次数 r 的概率服从参数为 m ( 样本容量)和 1/n ( 选取变量 i 的概率,任何时刻一个变量被选取是随机的)的二项分布。这一二项分布可以很好地近似为参数泊松分布,而且计算起来也更容易。
7. 见注 2。对于这种情况,λ 可以计算如下。不同于等概率情况,λi 在这里是不同的。首先,为了计算 λ,我们需要计算所有的 n = 2110 个参数 λi,这个工作量很大,但是这里包含了很多重复,这一特征可以用来简化计算。而且,让我们确定一些由五元组(n1,n2,n3,n4,n5)确定的十肽,由密码子的数量可知,它们的概率在所描述的十肽中分别为 1/64,2/64,3/64,4/64,5/64。并且有

种不同的十肽与五元组(n1,n2,n3,n4,n5)有关。这一数字解释了多肽中密码子的所有混编,也就是多肽中的氨基酸次序不需要被明确定义。它同样说明了这样一个事实,不止一个氨基酸能表现出其中的每一个概率(除了异亮氨酸,异亮氨酸是唯一一 个被 3/ 64 密码子编码的氨基酸)。我们提出的观点是,五元组包含了用来回答我们问题的关于十肽的所有信息。现在我们可以用 λ(n1,n2,n3,n4,n5)来替换 λi=(1-pi)m 的计算,因此,对于特定的十肽 i:
λi=λ(n1,n2,n3,n4,n5)=[ 1-p(n1,n2,n3,n4,n5)] m
这对于与十肽 i 相关的五元组(n1,n2,n3,n4,n5)是特定的。也就是说,对于 2110 个参数 λi,我们只需要计算 λi 中出现的不同值。λi 中一共有

个不同的值;这里,我们用了二项系数记号。
我们最后只用这 1001 个 λ(n1,n2,n3,n4,n5)值来计算,以及每个数值根据式(8.13 ) 所给出的重复次数。

这里第二,第三和第四步的求和都是定义在 8.1 中的五元组(n1,n2,n3,n4,n5)。也就是说,它们都是五套数字,这里 ni 是在 { 0,1,···,10 } 中的个数,因为它是—个十肽。同样的,p(n1,n2,n3,n4,n5)根据式
(8.16 ) 计算得到。最后一个方程给出了 λ 的近似值 ( 对于很小的 x,1 + x≈ex),这个运算要明显比从第二个方程到最后一个方程简单;通常,在计算机上计算,1 - p(n1,n2,n3,n4,n5)将趋近于 1。
8. 见注 5。这里唯一的不同是二项分布的基本事件概率不再是 1/n ( 等概率部分描述的概率),而是其他的一些基于不同的变量的概率 p。
9. 回顾显著性水平 α=0.05 的意义。这表示有 5% 的机会犯第一类错误,意味着假设为真却被拒绝。换句话说,这里有 1 : 20 的机会说明一个完美执行的试验有缺陷。
参考文献
1. Arnold, F. H. and Georgiou, G. (200 3 ) Directed Evolution Library Creation Methods and Protocols.Methodsin Molecular Biology 2 31, Humana Press, Totowa, NJ.
2. Arnold, F. H. and Georgiou, G. (2003) Directed Enzyme Evolution Screening and Selection Methods,Methodsin Molecular Biology 2 3 0, Humana Press, Totowa, NJ.
3. Moore, J. C. , Jin, H. M. , Kuchner, O. , and Arnold, F. H. ( 1 997) Strategies for the in vitro evolution ofprotein function —enzyme evolution by random recombination of improved sequences. /. Mol. Biol.272, 336-347.
4. Moore, G. L. and Maranas, C. D. (2000) Modeling DNA mutation and recombination for directed evolution experiments. J . Theor. Biol. 20 5 , 483-503.
5. Moore,G. L . ,Maranas,C. D . ,Lutz,S . ,and Benkovie,S. J. ( 2 0 0 1 ) Predicting crossover generation inDNA shuffling. Proc. NatL Acad. Sci. USA 98, 3226-3231.
6. Moore, G. L. and Maranas, C. D. ( 2002 ) Predicting out-of-sequence reassembly in DNA shuffling. /.Theor. Biol.2 1 9, 9-17.
7. Sun, F. ( 1 999) Modeling DNA shuffling./. BzoZ. 6 , 77-90.
8. Patrick, W. M. , Firth, A. E. , and Blackburn, J. M. (200 3) User-friendly algorithms for estimating complete?
ness and diversity in randomized protein-encoding libraries. Protein Eng. 16 , 451-457.
9. Bittker, J. A , I^e, R V. , Liu, J. M. , and Liu, D. R (2004) Directed evolution of protein enzymes using nonhomologous random recombinatioa Proc. Natl. Acad. Sci. USA 10 1, 7011-7016.
10. Gribskov, M. , Devereux, J. , and Burgess, R. R. (1 98 4 ) The codon preference plot: graphic analysis of protein coding sequences and prediction of gene expression. Nucleic Acids Res. 1 2, 539-549.
11. Virnekas, B. , Ge, L. , Pluckthun, A. , Schneider, K. C. , Wellnhofer, G. > and Moroney, S. E. ( 1 99 4 )Trinucleotide phosphoramidites : ideal reagents for the synthesis of mixed oligonucleotides for random mutagenesis. Nucleic Acids Res.22, 5600-5607.
12. Pelletier, J. N. > Arndt, K. M. , Pliickthun, A. , and Michnick, S. W. ( 1 999) An in vivo library-versus-library selection of optimized protein-protein interactions. Nature BiotechnoL 1 7, 683-690.
13. Braunagel, M. and Little, M. ( 1 997) Construction of a semisynthetic antibody library using trinucleotide oligos. Nucleic Acids Res. 25, 4690, 4691.
14. Gaytan, P. , Yanez,J . ,Sanchez, F . , and Soberon, X. ( 20 0 1 ) Orthogonal combinatorial mutagenesis: acodon-level combinatorial mutagenesis method useful for low multiplicity and amino acid-scanning protocols. Nucleic Acids Res. 29, E9.
15. Ross, S. ML ( 1 996) Stochastic Processes. 2nd ed. 9 John Wiley Sons, New York, NY.
16. Hogg, R. V. and Tanis, E. A. ( 1 98 3 ) Probability and Statistical Inference. 2nd eA. MacMillan, New York,NY.
17. Ross, S. M. (1998) A Fist Course in Probability. 5th ed. 9 Prentice Hall, Upper Saddle River, NJ.