如何用 Graphpad prism 8.0 进行非配对 / 独立样本（unpaired） t 检验？

在统计学分析里，最重要的元素是数据，因为数据的属性决定了用什么样的方式来比较数据，不同的数据比较方式就决定了统计分析方法以及对应的统计图。

今天继续给大家介绍一下 Graphpad 的统计分析功能之非配对 / 独立样本（unpaired）t 检验。

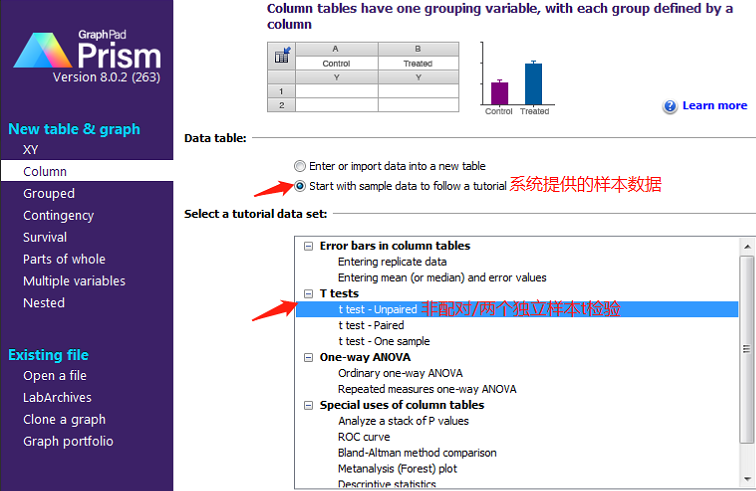
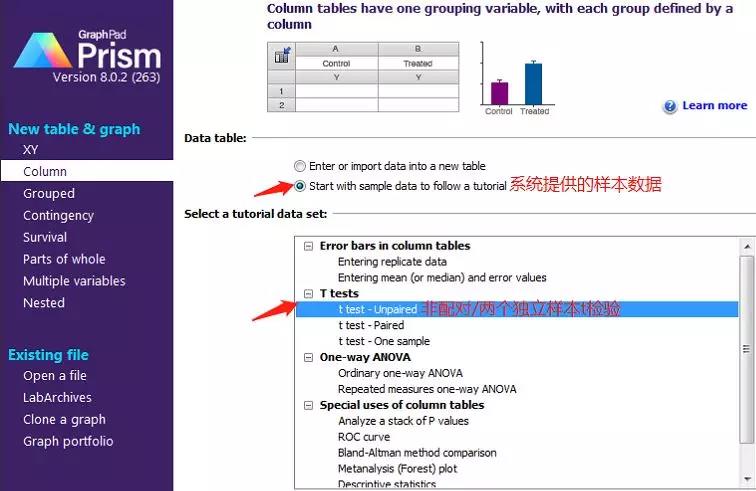
今天的演示直接以 sample data 来进行。

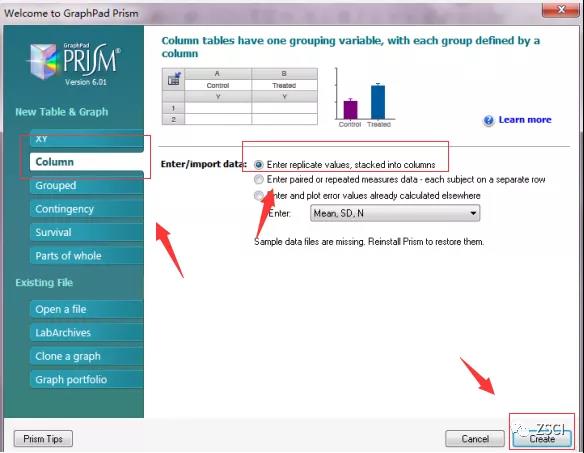
1. 点击 creat，生成一组系统示例数据。如下图

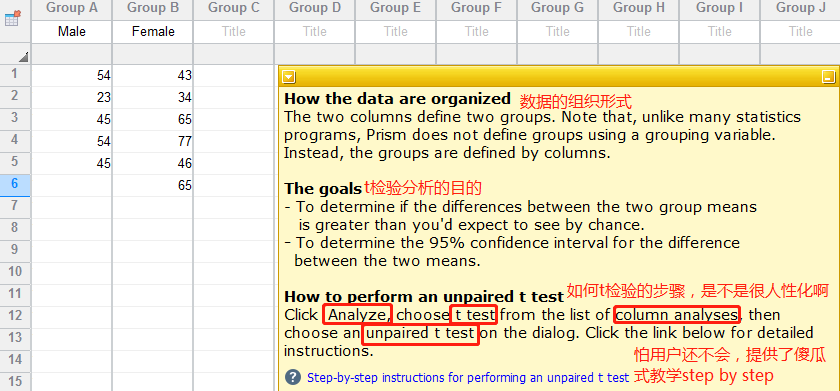
2. 点击 Analyze，也可以点击左侧的 Results 的 New Analysis，则会 creat a new analysis，选定 Column analyses 里的 t test (and nonparametric test)，再勾选右侧的 A:male 和 B:female

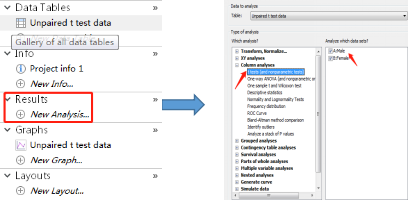
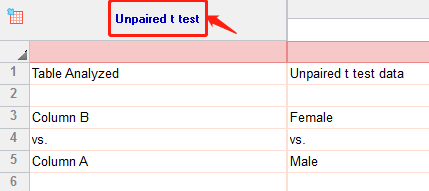
3. 点击 OK，得到下图，按照图示选择双尾（two-tailed）的 P value 和 95% CI 后，点击 OK

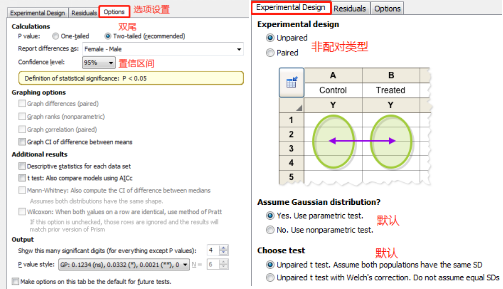
4. 得到本次 t 检验和 F 检验结果

①一般来说在双样本非配对 t 检验之前应先进行 F 检验，如上图 F 检验的 P 值为 0.6354＞0.05，说明无明显差异，说明 male 和 female 两组样本是方差齐。

②再来看 t 检验的 p 值为 0.2613＞0.05，同样无明显差异。

这里我们用 sample data 得到的两组数据的 F 检验 p＞0.05（方差齐），若实际操作过程中遇到 F 检验 p＜0.05 怎么办呢？

别急，听我说。若两组数据方差不齐，则需要校正。How？

点击 unpaired t test，选择 Experimental design 里的 choose test，按图示选择 welch 校正，得到校正后的新 P 值。

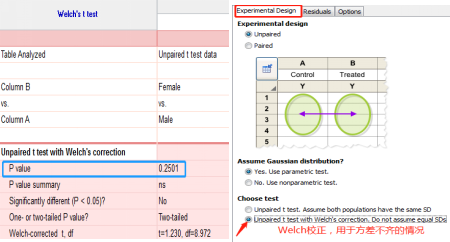
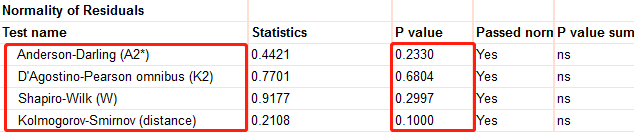
5. 我们先假设数据符合正态分布，按下图勾选，点击 OK 后出现对应 4 个 P 值，均＞0.05，则符合正态分布（Gaussian distribution）。

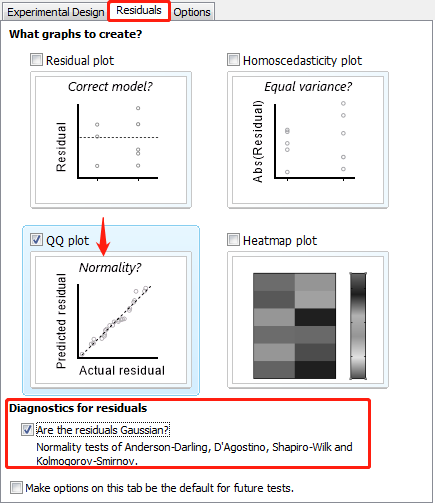
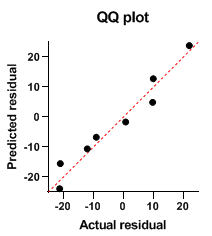
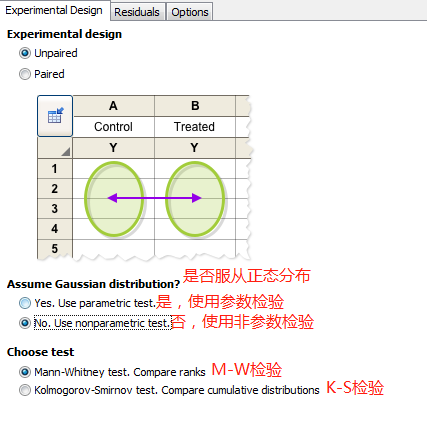
若实际数据不服从正态分布，多采用非参数检验。主要有两种非参数检验方法：

①「曼 - 惠特尼秩和检验」（Mann-Whitney test），它假设两个样本分别来自除了总体均值以外完全相同的两个总体，目的是检验两个总体均值是否有显著的差别。

② 正态性的 Kolmogorov-Smirnov 检验，这是一种基于 ECDF 的检验。

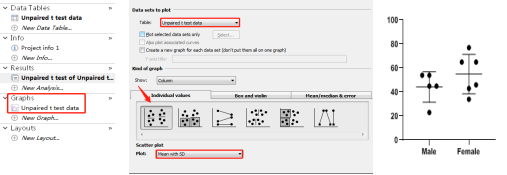
6. 完成了两组非配对 t 检验，得到了想要的 p 值，其实统计分析过程到这里就结束了，如果把相对应的统计图一起做出来岂不是更完美。点击下图示 Graphs---Unpaired t test data 按下图示选择，生成想要的图片。