基于 Excel 的简单相关与回归分析

基于 Excel 的简单相关与回归分析的基本原理是一般来说，生物类数据变量之间的关系属于非确定性的统计相关关系，如初生重与断奶重、身高与体重、背膘厚度与瘦肉率等。当只用一个自变量和线性关系就能描述另外一个因变量的变化时，称为简单线性相关或回归（simple linear correlation or regression）。

1．简单相关分析

相关分析（correlation analysis）主要用来研究呈平行关系的相关变量之间的关系。对两个变量间的直线关系进行相关分析称为简单相关分析（也叫直线相关分析）。若两个变量间存在简单相关关系，则其散点图大多围绕在一条直线的周围，呈现随着变量 x 值的增大，变量 y 值也增大的正相关趋势，或者随着变量 x 值的增大，变量 y 值随之减小的负相关趋势。相关系数（coefficient of correlation）是度量两个变量之间线性关系大小的指标。

总体相关系数的计算公式为：

通过对样本相关系数 r 的假设检验估计总体相关系数的显著性，从而确定总体变量之间是否具有显著的相关关系。简单相关分析的主要任务是研究两个变量之间线性相关的程度和性质。

2．简单回归分析

回归（regression）是由英国统计学家 Francis Galton 研究子代身高与父母身高时提出的。回归分析（regression analysis）主要用来研究呈因果关系的相关变量间的关系，其中表示原因的变量称为自变量（x），表示结果的变量称为因变量（y）。研究一个自变量与一个因变量的线性回归分析就称为简单回归分析。

回归分析表现的是两变量间比较严格的从属关系，是把非确定性的关系用严格的函数关系来进行研究。如果两变量的变化规律呈大致的直线关系，就应当把这条直线找出来并用一个回归方程来描述这条曲线，从而根据自变量 x 的变化来估计、预测因变量 y 的变化。y 对 x 的直线回归方程一般表示为：

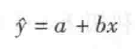
ŷ 是 y 的估计值，ŷ 和 y 间有一定的差异；x 为自变量，每一个 x_i 都对应一个 ŷ_i）；a 是直线在 y 轴上的截距，即当 x＝0 时的 ŷ 值；b 是回归系数，是直线的斜率，它是指当自变量 x 每变化一个单位时因变量 y 的平均变化量。

回归分析主要任务是揭示出呈因果关系的相关变量间的联系形式，建立它们之间的回归方程，利用所建立的回归方程，由自变量（原因）来预测、控制因变量（结果）。

需要特别指出的是，简单相关与回归具有紧密联系，但也有本质区别，主要表现在三个方面：第一，简单线性相关是变量之间呈线性关系的密切程度的表示，简单线性回归是变量在线性相关的基础上建立的变量之间的线性模型，也就是说相关不一定回归，反之回归则一定相关。第二，回归分析可对变量进行估计和预测，而相关分析则无此功能。第三，线性相关分析中的变量地位平等，都是随机变量，无主次因果之别，线性回归分析中的变量有自变量和因变量之分，且自变量一般属确定性变量如日龄，因变量属于随机变量如达某个日龄的体重。