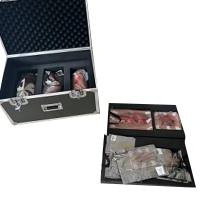
简介
Excel 电子表格在分析工具库中提供了进行非配对资料 t-检验的分析工具“ t-检验: 双样本等方差假设”。下面详细介绍利用 Excel 电子表格中的“t-检验: 双样本等方差假设”分析工具对表 3-4 中数据进行非配对资料 t-检验的具体操作方法。
原理
两个样本均数差异的假设检验就是根据两个样本平均数间的差值来推断这两个样本所属总体的总体平均数是否有显著差异。由于实验设计不同, 两个样本平均数差异的假设检验方法也不同。在进行两个样本的比较实验时, 一般有两种实验设计方法: 一种是两个样本的实验单位 (如实验动物) 是配对的, 所得到的两个样本观测值也是配对的; 另一种是两个样本的实验单位是相互独立的、非配对的, 所得到的两个样本观测值也是相互独立的。因此, 根据不同的实验设计方法, 两个样本平均数差异 t-检验的检验方法也可以分为配对数据 t-检验和非配对数据 t-检验。
(1)非配对数据t–检验的基本原理是
非配对数据t-检验的计算公式为:

将计算出的: 值与 2 个 t 临界值 (t0.05 , t0.01)进行比较, 作出推断。
材料与仪器
步骤
【例 3-2】为了研究某种新型药物对肿瘤的治疗效果, 将 20 只小白鼠随机分成试验组和对照组, 背部皮下注射 S180 瘤细胞稀液接种肿瘤, 试验组在接种肿瘤 24 h 后腹腔注射该新型药物制剂 5 mL, 对照组则注射 5 mL 生理盐水。连续给药 10 天后, 处死小白鼠, 测定瘤体大小 (cm) , 结果见表 3-4。试比较两组瘤体大小是否有显著差异。

(1) 数据输入
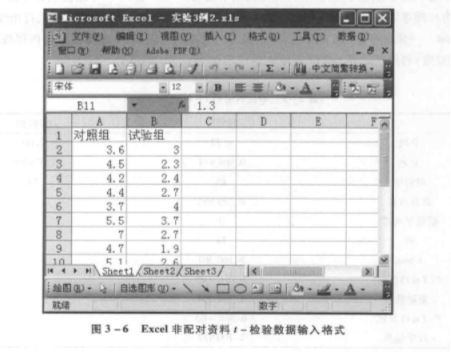
将对照组和试验组数据分别按列输人到 Excel 电子表格, 数据输入结果见图 3-6。
(2)操作步骤
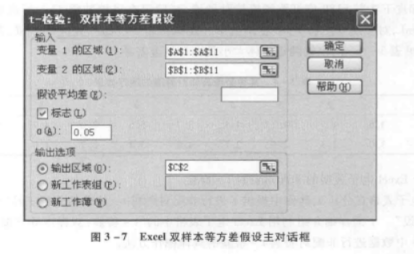
打开「*数据分析"对话框, 选定「t–检验: 双样本等方差假设」分析工具, 单击"确定"按钮, 打开「 t–检验: 双样本等方差假设」主对话框。在「t–检验: 双样本等方差假设」主对话框的输人部分中, 在"变量 1 的区域」中输人对照组数据所在区域 ($A$1:$As11 ) , 在「变量 2 的区域」中输人试验组数据所在区域 ( $B$1:$B $11 ) , 选定「标志"项, 显著水平α使用默认值 (0.05) 即可, 再选择一个输出区域 (例如$C$2) , 见图 3-7, 然后单击「确定"按钮, 执行非配对资料 t–检验。
(3)结果输出
Excel 电子表格非配对资料 t –检验输出结果见表 3-5。表 3-5 中输出项目分别为算术平均数 (即平均), 样本方差 (即方差), 样本容量 (即观测值)、合并方差, 假设平均差、自由度 (即 df ) ,t 值 (即 t Stat)、一尾概率值 (即 P(T<=t) 单尾)、一尾临界﹔值 (即﹔单尾临界), 两尾概率值 (即Р(T <= t) 双尾) 和两尾临界 t 值 (e 双尾临界)(本例为 to.escs, 的值)。

(4)结果分析
一般情况下,t–检验采用的是两尾检验, 因此我们可直接根据两尾概率值来进行推断, 如果两尾概率值大于 0.05, 表示差异不显著; 如果两尾概率值小于 0.05 , 表示差异显著; 如果两尾概率值小于 0.01 , 表示差异极显著。
来源:丁香实验