基于 Excel 电子表格的独立性检验

独立性检验就是检验按照两个方向来分类的数据资料是否具有相关关系， 若存在相关关系就说明它们之间不是独立的。按照两个方向来分类的数据资料通常以列联表 (contingencytable) 的形式出现， 根据行及列的分组数， 相继就出现了 2×2、R ×2，2xC 和 R×C 表。其中 2×2 列联表是最简单的列联表， 也称为四格表。

独立性检验的基本原理是检验按照两个方向来分类的数据资料是否具有相关关系， 若存在相关关系就说明它们之间不是独立的。按照两个方向来分类的数据资料通常以列联表 (contingencytable) 的形式出现， 根据行及列的分组数， 相继就出现了 2×2、R ×2，2xC 和 R×C 表。其中 2×2 列联表是最简单的列联表， 也称为四格表。

器材：Excel 电子表格

基于 Excel 电子表格的独立性检验的实验步骤如下：

【例 4－3】为了分析新措施对防治仔猪白痢的效果， 试验结束后得到如下资料 （表 4－8）。试检验新措施对防治仔猪白痢是否优于传统措施 （对照）。

（ 1） 数据输入

先根据独立性检验理论值的计算公式：

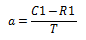
计算出 a 格的理论值为 123； 然后根据相应公式计算出 b ，e ，d 格的理论值， 分别为 27，123 和 27。由于本例中的 df＝1 ， 需要进行连续性校正。但是，Excel 电子表格无法进行连续性校正， 因此需要手工进行校正， 只要将观察数和相应理论数中较大的值减去 0.5 即可。将校正后的观察数和理论数输入到 Excel 电子表格中， 见图 4－11。

（2）操作步骤

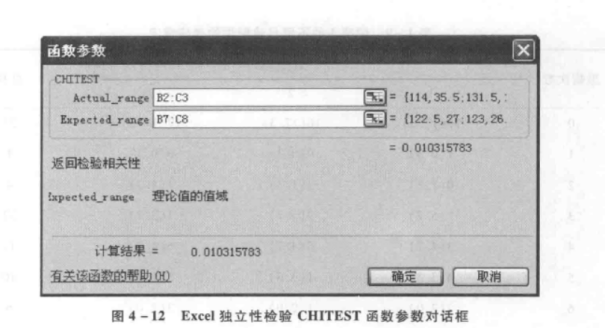
打开「插人函数＂对话框， 选择 CHTTEST 粘贴函数， 打开「函数参数＂对话框， 见图 4－12。在「函数参数」对话框的观测值值域「 Actual＿range」中输人观察数所在区域 （B2:C3 ） ， 在理论值值域「Expected＿range」中输入理论数所在区域 （B7:C8）， 单击「确定」。

（3） 结果输出

输出结果为 0.0103。

（4） 结果分析

输出结果为概率值即 0.0103 ， 小于显著水平 0.05， 即差异显著， 表明新措施对防治仔猪白痢显著优于传统措施。

【例 4－4】现有 3 组奶牛， 每组 39 头， 分别饲喂 3 种不同日粮， 记录每头奶牛的患病次数， 数据见表 4－9。试问奶牛的患病次数是否与所喂日粮有关。

（1） 数据输入

首先根据理论数的计算公式：

计算出相应的理论数， 写在表 4－9 中观察数后的括号中。

由于表 4－9 中许多格子的理论次数小于 5， 在处理这类资料时， 可将邻近组的数据进行合并， 合并结果见表 4－10。将表 4－10 中的数据输入到 Excel 电子表格中， 结果见图 4－13。

（2）操作步骤

打开「插入函数」对话框， 选择 CHITEST 粘贴函数， 打开「函数参数」对话框。在「函数参数」对话框的观测值值域「 Actual＿range」中输入观察数所在区域 （B4:D7） ， 在理论值值域「Ex－pected＿range」中输入理论数所在区域 （B13:D16） ， 单击「确定」。

（3） 结果输出

输出概率值为 0.1011。

（4） 结果分析

厩率值为 0.1011， 大于显著水平 0.05， 即差异不显著， 表明日粮与奶牛患病次数无关。