基于 Excel 的非参数检验

非参数检验的基本原理是非参数检验是在总体分布不服从正态分布且分布情况不明时，用来检验数据资料是否来自同一个总体假设的一类检验方法。在检验时不需要利用总体参数（如平均数、标准差等）的信息，主要是利用样本数据之间的大小比较及大小顺序，对两个或多个样本所属总体是否相同进行检验。

1．两个样本资料的非参数检验

根据实验设计方法的不同，两个样本资料的非参数检验方法可分为两个相关样本的非参数检验和两组非配对（独立）样本的非参数检验。两个相关样本常常是从一个对象身上测得的两个或多个指标，将这些指标分别看做抽样，这时由于一个指标的抽样会对另一个指标的抽样产生影响，两组样本就不是独立的，而是具有相关性。两组独立样本就是从一个总体中抽取样本对从另一个总体中抽取样本没有影响。

（1）两个相关样本的非参数检验

两个相关样本的非参数检验要有符号检验（sign test）和 Wilcoxon 符号秩和检验。

① 符号检验 符号检验是根据样本各对数据大小之差的正负符号来进行检验，不考虑其差值的大小，每对数据之差为正值用「＋」表示，负值用「-」表示，然后通过对比符号「＋」和「-」的个数进行统计推断。其检验的基本思想与原理是假定两个样本所属总体服从相同的分布，则正号或负号出现的概率应该相等，若不能完全相等，至少不应相差过大，当其相差超过一定的临界值时，就认为两个样本所属总体有显著差异，它们不服从相同的分布。其公式如下：

将用样本得到的γ值与临界值γ0.05（N），γ0.01（N）比较，做出统计分析。符号检验也可以采用 x 求解，其公式如下：

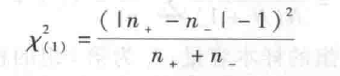
将计算出的 x² 值与 x² 临界值（x²0.05，x²0.01）进行比较，然后作出推断。

② Wilcoxon 符号秩和检验 Wilcoxon 符号秩和检验在符号检验的基础上进行了改进，考虑了差值的大小。每对数据之差为正值用「＋」表示，负值用「-」表示，然后将差值绝对值数据进行升序排列，并求出相应的秩（如果存在同分秩，则需要进行同分修正）。将正负秩次分别相加，求秩和用 T，表示正秩次之和，用 T＿表示负秩次之和，取秩和绝对值小者 Tn＝min（T，T＿）作为检验统计量。根据样本容量对子数 n 查符号秩和检验表得显著性水平为 5％ 与 1％ 的临界 T 值，用 T。值与临界值比较，当小于某水平的临界值时，就表明在这一显著水平下差异显著。5％ 与 1％ 显著水平的临界 T 值可由以下公式计算：

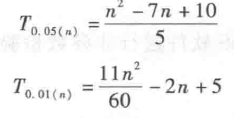
当 n 无穷大时，检验统计量 T 值的抽样分布趋向于正态分布 N（μ，σ²）。因此，只要 n 达到适当大（一般情况为 n ≥ 19）时，就可以用 Z 检验进行近似的检验，其计算公式如下：

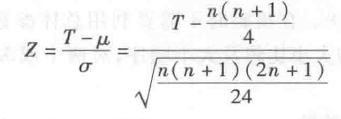
（2）两组非配对（独立）资料的秩和检验

两组非配对资料的秩和检验是抽自两个独立总体的两个独立样本之间的比较，该检验又称为 Mann-Whitney（曼-惠特尼）秩和检验。

将两组数据合并，按数值大小由小至大排列，每一数值对应的顺序号就为该数值的秩次，数值最小的秩次为 1，数值最大的秩次为两组样本容量之和，即「n₁＋n₂」，相同数值计算平均秩次；将两组的秩次分别相加求和，以样本容量最小组秩和作为 T 值；用 T 值与根据 n，及 n₂ 查成组资料秩和检验表所得临界值比较，进行显著性分析。

非配对资料秩和检验表只列出了 n₁ 及 n₂ 小于 10 的情形，当 n₁ 及 n₂ 大于 10 时，秩和 T 近似服从正态分布，因而可以用 Z 检验法近似地进行检验，其计算公式如下：

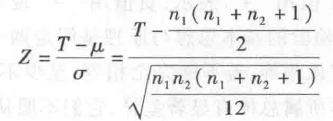
2．多个样本资料的秩和检验

多个样本资料的秩和检验法又称为 Kruskal-Wallis 检验法，该法利用多个样本的秩和来推断它们分别代表的总体分布是否相同。由于该检验统计量用 H 表示，所以也称为 H 检验。其计算公式如下：

其中：N 为观测值总数；n；为第 i 组的样本容量；T，为第 i 组的秩和，每个观测值的秩次的计算方法与两组非配对资料的秩和检验相同。当资料中的分组数 k ≥ 3 时，且每组样本容量大于等于 5 时，统计量 H 的抽样分布近似于 df＝k-1 时的 x² 分布，于是可以用 df＝k-1 时的 x² 值作为临界值来判断各组秩和的差异是否显著。对于 k＝3，且每组含量小于 5 时，需要用 Kruskal-Wallis 的正确概率表进行比较。如果在样本中有较多的平均秩次，应对 H 值进行校正，校正公式如下：

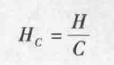
其中：C 为校正系数，计算公式如下：

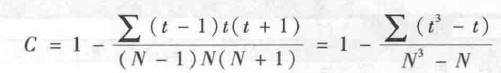
其中：t 为具有相同数值的个数。