基于Excel的方差分析

单因素方差分析的基本原理是当需要对 k（k≥3）个总体平均数进行比较时，将产生 1/2k（k-1）个差数，如果要对这些差数逐一进行检验，会随着 k 的增加而大大增加犯Ⅰ型错误的概率，导致实验误差增大、估计精确度降低。因此，不能直接应用 t-检验或 u 检验进行两两平均数之间的假设检验。统计学家为此提出了检验 k≥3 系统中是否存在显著性影响因素的方法，其实质就是对观测值变异原因的量化分析，并称其为方差分析（ANOVA）。
（1）线性模型与基本假定
假设某单因素实验有 k 个处理，每个处理有 n 次重复，共有 kn 个观测值。这类实验资料的数据结构如表 5-1 所示。

（2）平方和与自由度的剖分

①总平方和的剖分 在表 5-1 中，反映全部观测值总变异的是各观测值 x，与总平均数 x 的离均差平方和，记为 SSr，则有：

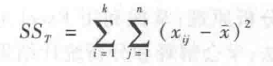
分解后得：

② 总自由度的剖分 在计算总平方和时，资料中的各个观测值受「离均差之和为 0」这一条件的约束，故总自由度等于资料中观测值的总个数减 1，即总自由度 dfT＝kn-1。而总自由度可以剖分为两部分：处理间自由度 dft＝k-1 和处理内自由度 dfe＝kn-k＝k（n-1）。各部分平方和除以各自的自由度便得到总均方、处理间均方和处理内均方，分别记为 MST、MSt 和 MSe。

（3）F 分布与 F 检验

① F 分布 在一正态总体 N（μ，σ2）中，随机抽取样本含量为 n 的样本 k 个，将各样本观测值整理成表 5-1 的形式。因此，可以根据公式计算出的和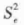都是误差方差σ² 的估计量。以为分母，为分子，求其比值。统计学上把两个均方之比值称为 F 值，即：

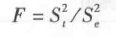
F 具有两个自由度：df1＝dft＝k-1，df2＝dfe＝k（n-1）。若在给定的 k 和 n 的条件下，继续从该总体进行一系列抽样，则可获得一系列的 F 值。这些 F 值所具有的概率分布称为 F 分布。可以根据 F 临界值表查出临界值 F0.05 和 F0.01。
②F 检验 用 F 值出现概率的大小推断两个总体方差是否相等的方法称为 F 检验。在单因素方差分析中，无效假设为 H0：μ1＝μ2＝…..＝μk，备择假设为 HA：各μi 不全相等。若 F＜F0.05（df1,df2），即 P＞0.05，接收 H0，说明各处理间差异不显著；若 F0.05（df1,df2）≤F＜F0.01（df1,df2），即 P≤0.05，否定 H0，接受 HA，说明各处理间差异显著；若 F≥F0.01（df1,df2），即 P≤0.01，否定 H0，接受 HA，说明各处理间差异极显著。

（4）多重比较

①最小显著差数法 最小显著差数法（least significant difference，LSD）是最简单的一种多重比较方法，利用 LSD 法进行多重比较的步骤为：列出平均数的多重比较表，比较表中各处理按其平均数从大到小自上而下排列；计算最小显著差数 LSD0.05 和 LSD0.01；将平均数多重比较表中两两平均数的差数与 LSD0.05、LSD0.01 比较，作出统计推断。
LSD 法进行多重比较的尺度公式为：

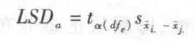
② Duncan 法 Duncan 法是把平均数的差数看成是平均数的极差，根据极差范围内所包含的处理数（称为秩次距）k 的不同而采用不同的检验尺度，以克服 LSD 法的不足。这些在显著水平α上依秩次距 k 的不同而采用的不同的检验尺度也叫做最小显著极差 LSR。
计算公式为：

两因素方差分析的基本原理是当被研究性状同时受到两个因素的影响，需要同时对两个因素进行分析时，可进行两因素方差分析。各影响因素的相对独立作用称为该因素的主效应（main effect）；某一因素在另一因素的不同水平上所产生的效应不同，则两因素间存在交互作用，简称互作（interaction）。因素间互作显著与否关系到主效应的利用价值，若互作不显著，则各因素的效应可以累加，各因素的最优水平组合起来，即为最优的处理组合；若互作显著，则各因素的效应就不能直接累加，最优处理的选定应根据各处理组合的直接表现选定。

（1）无重复观测值的两因素方差分析

无重复观测值即每个处理未设重复，即假定 A 因素有 a 个水平，B 因素有 b 个水平，每个处理组合只有 1 个观测值。无重复资料的数据结构见表 5-2。

两因素方差分析中观测值的线性模型为：

无重复资料两因素方差分析的结果可以汇总如表 5-3 的形式。

（2）重复观测值的两因素方差分析

无重复观测值进行两因素方差分析，所估计的误差实际上就是这两个因素的互作，这个结果只是在两个因素不存在互作，或互作很小的情况下成立。但是，如果存在两个因素的互作，实验设计中就必须设计重复观测值，可同时估计互作以及误差。具有等重复观测值的两因素实验的典型设计是：假定 A 因素有 a 水平，B 因素有 b 水平，每一不同因素水平的组合设计 n 次重复，资料模式见表 5-4。

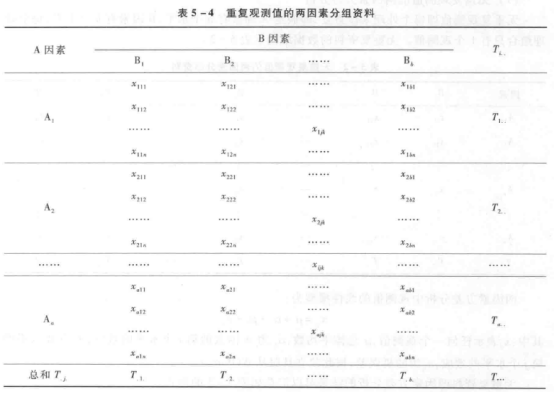
重复观测值两因素资料的线性数学模型为：

重复观测值两因素方差分析的结果可以汇总如表 5-5 的形式。