基于 SPSS 的多元线性回归与曲线回归分析

基于 SPSS 的多元线性回归与曲线回归分析的基本原理是：

1．多元线性回归分析

多元线性回归（multiple linear regression）分析是分析多个自变量与一个因变量间数量关系的方法，并可进行回归诊断。多元线性回归分析的原理与一元线性回归分析基本相同，分析的目的是建立由多个自变量预测和控制因变量的多元线性回归方程，即确定多个自变量对因变量的单独效应和综合效应，并对上述单独效应和综合效应进行显著性检验，选择仅对因变量有显著效应的自变量建立最优多元线性回归方程。

设因变量 y 与自变量 x1，x2，，xm 间存在线性关系，其数学模型为：

用于多元线性回归分析的样本数据是由 n 个个体实际测定而得，即有 n 组观测值，每组数据均包含有 1 个因变量和 m 个自变量的测定值，每组数据构成一个样本点，其数据结构如表 8-1 所示。

由 n 组实际观测数据计算得到的一个 m 元线性回归方程可由下式表示：

其中：ŷ 是多元线性回归的估计值，b0，b1，b2，····，bm 是 β0，β1，β2，，βm 的最小二乘偏回归系数估计，它们应使离回归平方和 Q 达到最小。即：

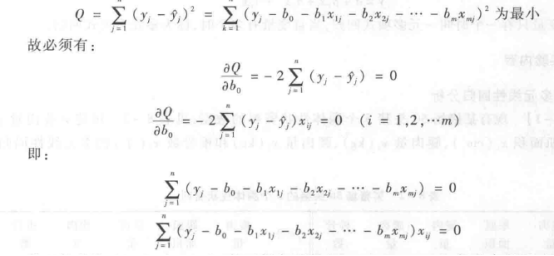
整理得到关于 b0，b1，b2，，bm 的正规方程组（normal equations），解此方程组，可得 b0，b1，b2，，bm，于是得到 m 元线性回归方程为：

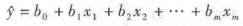
常用统计软件中多元线性回归分析正规方程组在求解 bo，b1，b2，···，bm 时，均采用矩阵法，所以不必考虑计算的问题。多元线性回归方程是否有意义，采用 F-检验，当检验显著存在多元线性关系后，再检验偏回归系数的显著性，可以用 t-检验也可用 F-检验，淘汰不显著的自＼rac3 变量，并最终建立最优多元线性回归方程。

2．曲线回归分析

曲线回归分析是当两个相关变量的实际观测值的关系为曲线时，建立曲线回归方程以揭示变量间的内在联系和变化规律。曲线回归分析可分为两种情况，即已知曲线类型和未知曲线类型的回归分析。

（1）已知曲线类型

所谓已知曲线类型，是指可以根据理论、经验或对样本数据的分析来确定的曲线类型，也就是根据专业知识和散点分布的趋势来确定曲线类型，这一类曲线最大的特点是曲线函数已知。

常见的已知曲线类型有双曲线函数模型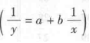；指数函数模型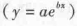；对数函数模型；幂函数模型（y＝ax^b）；Logistic（S 型）生长曲线模型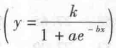等。

（2）未知曲线类型（多项式回归）

当找不到已知的曲线函数拟合实测点的分布趋势时，这类曲线叫未知曲线类型，此时最常用的方法就是利用多项式回归来拟合实测点的分布，也可以利用多项式回归，通过逐步增加多项式的高次项来拟合，直到满意为止。其原理是，任何函数都可用多项式来近似，即：

当自变量只有一个时叫一元多项式回归，当自变量有多个时，称为多元多项式回归。